Tree Model in ML

Tree Model in Machine Learning

Hope somebody have heard about Decision Tree, CART, Random Forest, GBDT, et.al. Actually, all of those algorithms are based on Tree. How could tree would help computes to do classification or regression tasks? Let’s explore it:

Define Task

Before exploring all of those tree models, let’s define the task which we would handle by using above algorithms.

Classification Task

Suppose, we want to predict whether a person like playing computer games according to gender, age, occupation, et.al.

Then the problem set is: Given \(X\in F_{m\times n}, Y \in {like, dislike}\) to predict person whether like computer games.

Regression Task

Nowadays in China, the house pricing is the most concerned topic. Suppose we have a lot of house parameters such as size, the distance btw mall, et.al. Then we need to predict houses’ price according to historic data.

Then the problem set: Given \(X\in F_{m\times n}, Y\in R_{1\times n}\) to build a model to predict house’s price according to \(X,Y\)

Decision Tree

Let’s look at the following picture(copy from xgboost):

img

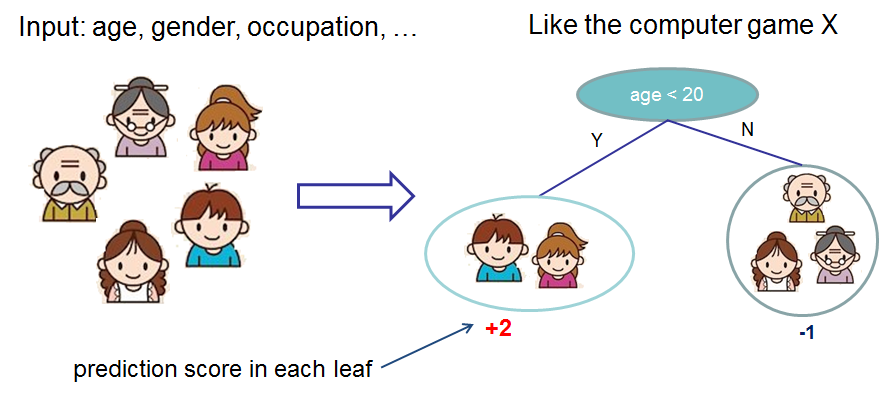
Then you would know the process of decision tree. We need to choose a feature to split the whole data sets until the tree node cannot to split. And the critical problem is how to choose the splitting feature at each step.

Impurity

Suppose the whole dataset is impure due to there are too many classes(like, dislike). At each step, we need to choose a feature which could increase the purity after splitting the dataset according to the selected feature. Because the split node would contain small classes.

• Information Entropy

  Entropy is used to define the confusion degree of a system. In information theory, Shannon used it to define the information. The entropy is bigger, the information is more. We could use it to define the impurity. The entropy is bigger, the impurity is bigger. \[ Entropy(X) = \sum_{i=0}^c -p_i \log p_i \] \(p_i = \frac{num\ of \ class\ i}{total\ num}\)

• Gini Coefficient

  Gini coefficient is used to define the income equality. It is bigger then the income is more inequality. So could also use it to define the impurity. The gini index is bigger, the impurity is bigger. \[ Gini(X) = 1- \sum_{i=1}^{c}p_i^2 \] , \(p_i\) is the same as above.

Information/Purity Gain

Above we have talked about how to define the impurity. So we split the dataset based on the feature which could most increase the dataset’s purity. No matter entropy or gini index, after splitting they would decrease. So the information gain is: \[ Gain(X, f) = Impurity\_before - Impurity\_after \]

\[ Impurity\_after = \sum_{v=1}^V \frac{|D_v|}{|D|} impurity\_of\_v \]

So at each step , we choose the biggest Gain feature to split the tree node until reach some condition(depth, leaf node constriction, et.al.). After the tree built, we could use the model to do classification, just like a marble flow from the root node to leafs. Each leaf represents one class/label.

img

Note:

• Let’s think about one index feature, such as there 100 sample, then their index feature is 1,2,…,1001,2,…,100 . The index feature would lead to best split. But it is of course not a good choice. Actually Information Gain prefers the more value features.
• How could we deal with numerical features? Bucketing

Conclusion

Now let conclude the decision tree algorithm:

• Compute current impurity (Entropy or Gini Index), impurity_before
• Select a feature and compute the impurity, impurity_after
• Repeat Step 2 for all features
• Compute the information gain for all features
• Select the biggest information gain feature to split current node
• Repeat above steps until cannot be split

Regression Tree

Above we have explored how decision tree do classification tasks. Now we will go through the regression task. Let’s think about the difference between classification and regression. The most important is the class/label. Classification task would have fixed values, but for regression it would be infinity. In decision tree, we could use the fixed classed to compute the impurity and found best split. In regression, how could we split the tree? And how to measure the impurity after splitting?

In regression tree, we often use mean square error (hereinafter is MSE) to measure the impurity. Of course, we could use other variants of MSE, such as mean absolute error(hereinafter MAE), friedman_mse, et.al.

Then when do regression, after data points flowed to leaf nodes, the predicted result is the average label of leaf node. That is: \(result=average(leaf(y))\)

That’s easy!!!

Ensemble Learning

Bias-Variance Decomposition

Define following variables:

• \(E(f;D)\) : error between actual value and predicted value.
• \(f(x;D)\) : predicted value on train set D
• \(f(x)=ED[f(x;D)]\): expectation of \(f(x;D)\) on different datasets
• \(y_D\): label on train set D
• \(y\): actual label of the true distribution for whole data set

For regression, we could decompose \(E(f;D)\) as follows: \[ E(f;D) = E_D[(f(x;D)-f(x))^2] + (f(x)-y)^2 + E_D[(y_D-y)^2] \] So \(var = E_d[(f(x;D)-f(x))^2]\) is the variance caused by the limited train set. And \(noise = E_D[(y_D-y)^2]\)

which caused by data, and we cannot get over it.

\(bias = (f(x) - y)^2\) is the bias between predicted value of model and actual label.

That is: \(E(f;D) = bias + var + noise\)

So we could improve our model from two points: bias and var

Bias-variance Trade-off

Intuitively, bias represents the error between model predicted value and the train set’s value. variance indicates the error between train set’s value and the actual value. When bias decreased(model fits train set better), variancewould increase. Because when train more, the data quality could effect accuracy more. We called this is Bias-variance trade-off

bias variance trade off

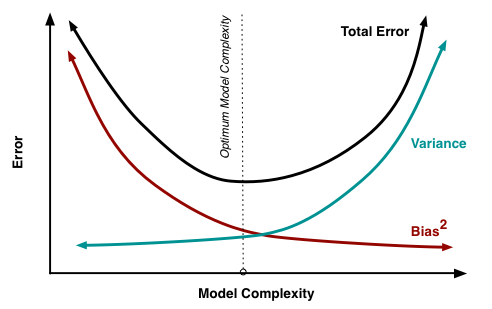
Bagging

Bagging is the method which improve models from var point of view. It increases the train data sets’ diversity by sub-sampling both on instances and features. The most popular Tree Model bagging algorithm is Random Forest.

Random Forest & Extremely Randomized Trees

A random forest is a meta estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and use averaging to improve the predictive accuracy and control over-fitting. Please refer to the Bias-variance decomposition in Random Forests to get more about why using more models ensemble could decrease the variance.

Random Forest

Boosting

Until now, we could improve our model’s accuracy by decreasing variance. Are there any methods which could both decrease variance and bias? Of course, boosting could make this dream comes true.